Physics 101

Course sections

Section 1
Forces
1
Forces

Forces

Forces

Force

  • It is the product of mass and acceleration of an object
  • It is a vector quantity
  • F = m x a
  • SI unit is N or kg m/s2
  • An applied force can change the shape, size, speed, and the direction of movement of an object, but cannot change its mass.

Net Force

  • When acting in the same direction, the forces are simply added together to obtain the net force.
  • Calculate the acceleration of the object –

  • \sum F = F_{1} + F_{2}
  • F_\textup{Net} = 30 - 10 = 20 N (\textup{to the right})
  • F_\textup{Net} = m \times a
  • a=\frac{F_\textup{Net}}{m}
  • a=\frac{10}{10}=2 \frac{m}{s^{2}} \textup{(to the right)}

Translational Equilibrium

  • Translational equilibrium occurs when along a straight path, net force is zero.
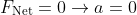
  • F_\textup{Net}=0\rightarrow a=0
  • a=\frac{v-u}{t}=0
    • If 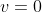v=0 then u = 0 and the body is at rest.
    • If 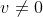v\neq 0, then v = u and the body moves at a uniform velocity.
  • So, to be in translational equilibrium, either the object should be at rest or moving with uniform velocity.

Friction, Air Resistance, and Terminal Velocity

Friction

  • Frictional forces are resistive forces acting on a body, working to oppose its relative motion.
  • Its directed to impede motion, i.e. its direction is always opposite to the motion of an object.
  • The energy lost is converted to heat and sound, heating the objects.
  • It arises due to interlocking between two surfaces in contact.
  • Presence of a liquid or lubricants reduces the frictional force between two surfaces in contact.

Air Resistance

  • Air resistance arises due to fluid friction – i.e. when an object moves through a fluid, the frictional force it experiences is known as air resistance
  • It increases with speed
  • When a falling object speeds up enough to cause the air resistance to equal the force of gravity, the constant speed is known as terminal velocity.
  • At the terminal velocity,
    • Body is in equilibrium,
    • Net force on the body is 0N
    • Acceleration is 0 m/s^{2}
    • Speed is constant

Hooke’s Law

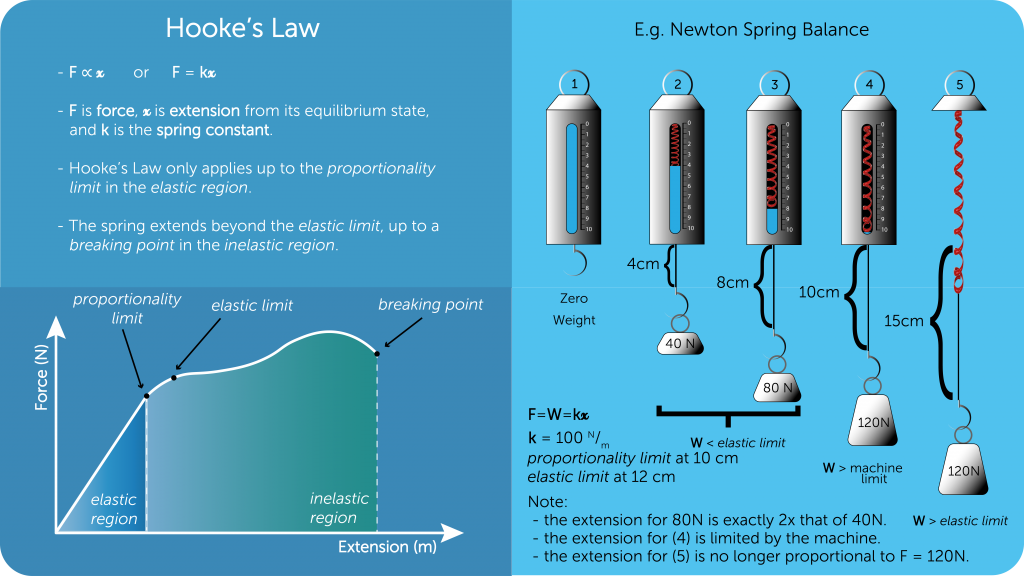
Centripetal Acceleration

  • A body moving in a circular path with a constant speed is accelerated because of its changing direction, i.e. velocity is not constant.
  • This acceleration is perpendicular to its direction of motion at all times.
  • Thus, the net force is perpendicular to the motion at all times in circular motion.

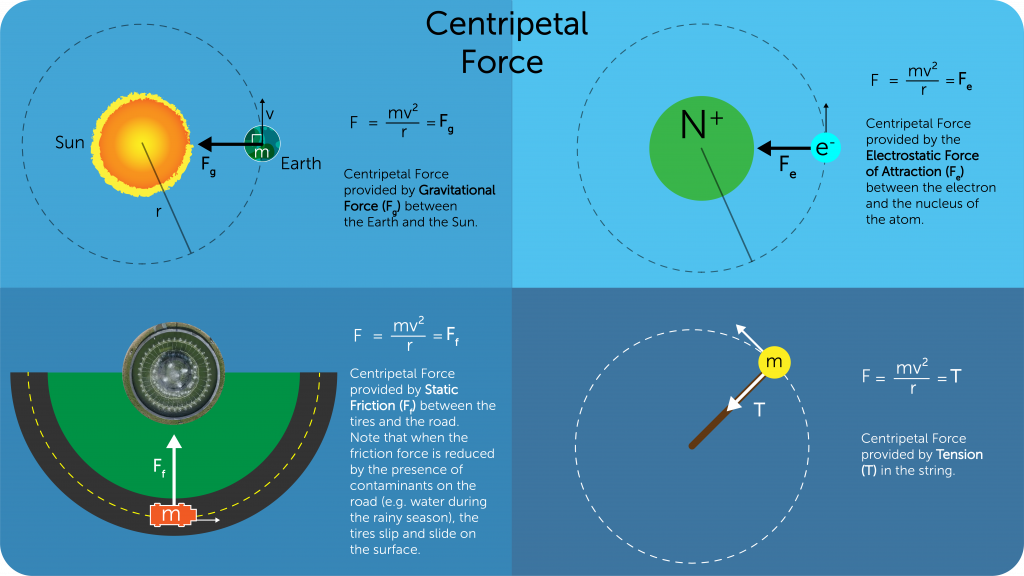
Moment of a Force

  • It is the product of force and the perpendicular distance from the line of action of the force to the pivot about which the object is rotating
  • It is a vector quantity
  • M = F \times d_{N}
  • SI unit is N\cdot m
    • Not \textup{Joule (J)}!

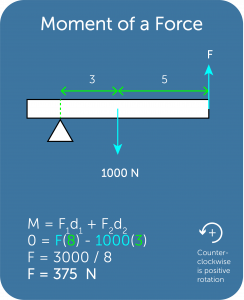
Rotational Equilibrium

  • To be in complete equilibrium, both the net force and net moment on an object must be zero.
  • This means the object must be in translational and rotational equilibrium.
  • For rotational equilibrium, i.e. zero or constant rotational speed
    • Total clockwise Moment Total anticlockwise Moment
  • The following are multiple examples depicting this concept

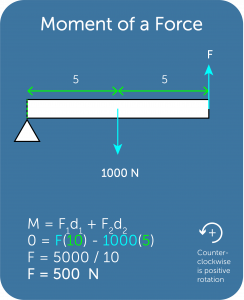
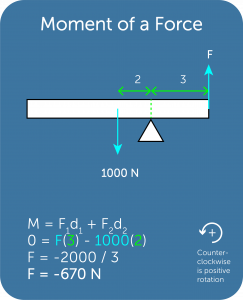
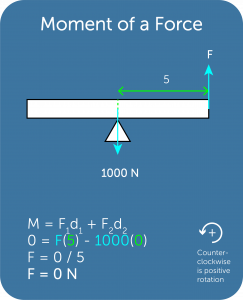
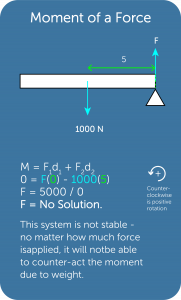
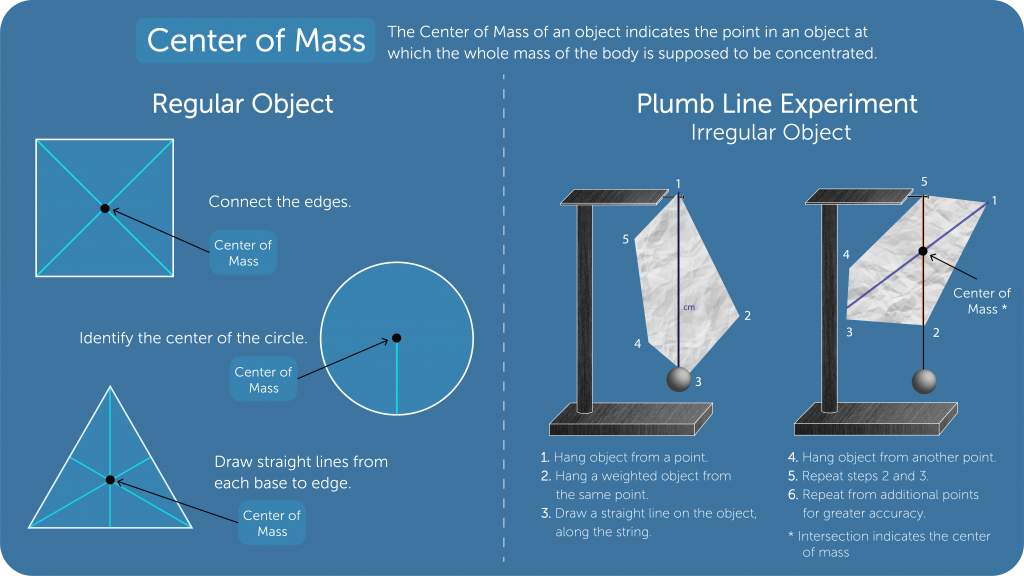
Center of Mass

  • It is a point in an object at which the whole mass of the body is supposed to be concentrated.

Scalars and Vectors

Scalars

  • A scalar quantity only consists of a magnitude
  • It is independent of direction.
  • Scalars can be algebraically added
    • 2 kg of apples + 3 kg of apples = 5 kg of apples

Vectors

  • A vector quantity consists of both a magnitude and a direction.
  • Vectors follow the rules of vector addition,
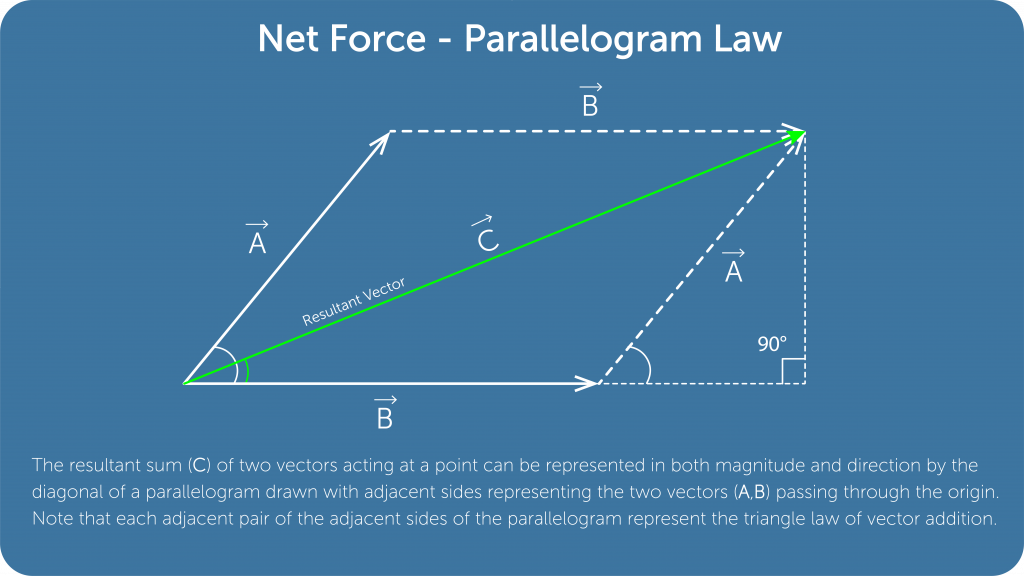
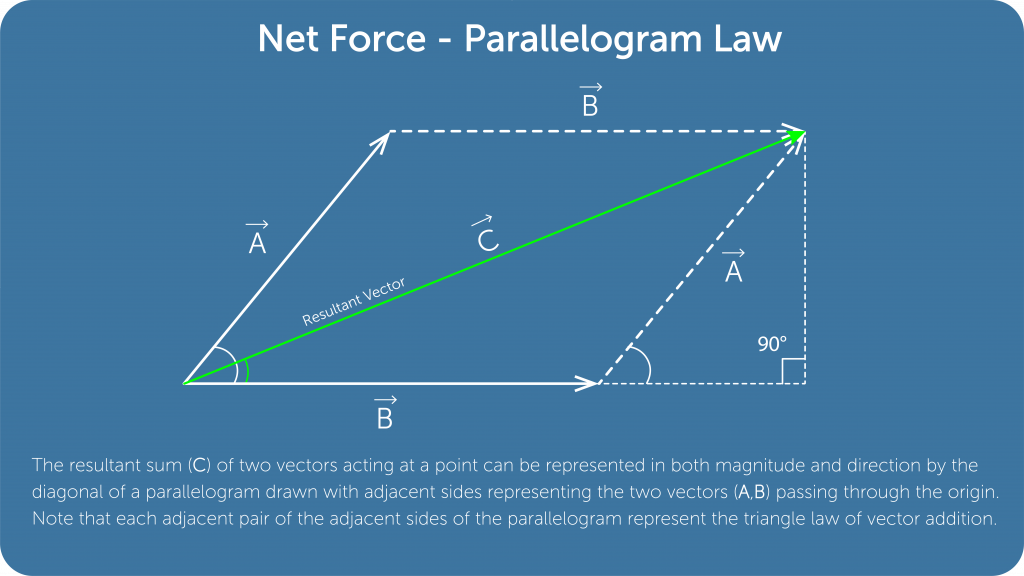
  • Methods such as the parallelogram law of vector addition can be used to determine the resultant of two vectors.
Scalar Quantities Vectors Quantities
Mass Weight
Length Force
Time Acceleration
Temperature Electric Field
Distance Magnetic Field
Speed Gravitational Field
Work Displacement
Pressure Moment
Energy Momentum
Potential Difference Impulse
Electric Charge Velocity
Current
Power
Resistance

Parallelogram law of Vector addition