Course sections

Section 1

Motion

Motion

Motion

Distance:

Length of the actual path covered
It is a scalar quantity
SI unit is meter

Speed:

It is the rate of change of distance
It is a scalar quantity
$\textup{Speed (v)} = \frac{\textup{Distance (S)}}{\textup{Time (t)}}$
SI unit is m/s

Average Speed:

It is the average speed over a time interval
$\textup{Average speed (v)} = \frac{\textup{Total Distance (d)}}{\textup{Total time(t)}}$
- u is the initial speed
- v is the final speed

Displacement and Velocity

Displacement

Length of the shortest path between two points
It is a vector quantity
SI unit is meter m.

Velocity

It is the rate of change of displacement
It is a vector quantity
$\textup{Velocity (v)} = \frac{Displacement (s)}{Time (t)}$
SI unit is m/s

Average Velocity

It is the average velocity over a time interval
$\textup{Average Velocity (v)} = \frac{ \textup{Total Displacement (s)}}{\textup{Total Time (t)}}$
$\textup{Average Velocity (for constant acceleration)} = \frac{u+v}{2}$
- u is the initial velocity
- v is the final velocity

Acceleration:

The rate of change of velocity is called acceleration
It is a vector quantity
$a = \frac{v-u}{t}$
u is the initial velocity
v is the final velocity
SI unit of is m/s² or N/kg

Constant Acceleration

Phase 1: Constant Positive Acceleration
- Velocity increases linearly with time:
  - $v = \frac{d_{2}-d_{1}}{t_{2}-t_{1}} =$ gradient of the distance-time graph
  - $a = \frac{v_{2}-v_{1}}{t_{2}-t_{1}} =$ gradient of the speed-time graph
- Displacement increases with time squared:
  - Area under the velocity-time graph is the displacement
  - Area under the speed-time graph is distance
- Example: Freefall under the influence of gravity
Phase 2: Constant Zero Acceleration
- Velocity remains constant with time:
- Displacement increases linearly with time:
Phase 3: Constant Negative Acceleration (Constant Deceleration)
- Velocity decreases linearly:
- Displacement increases with negative of time squared:
- This is equivalent to that of a body in freefall under the effect of gravity without air resistance

Changing Acceleration

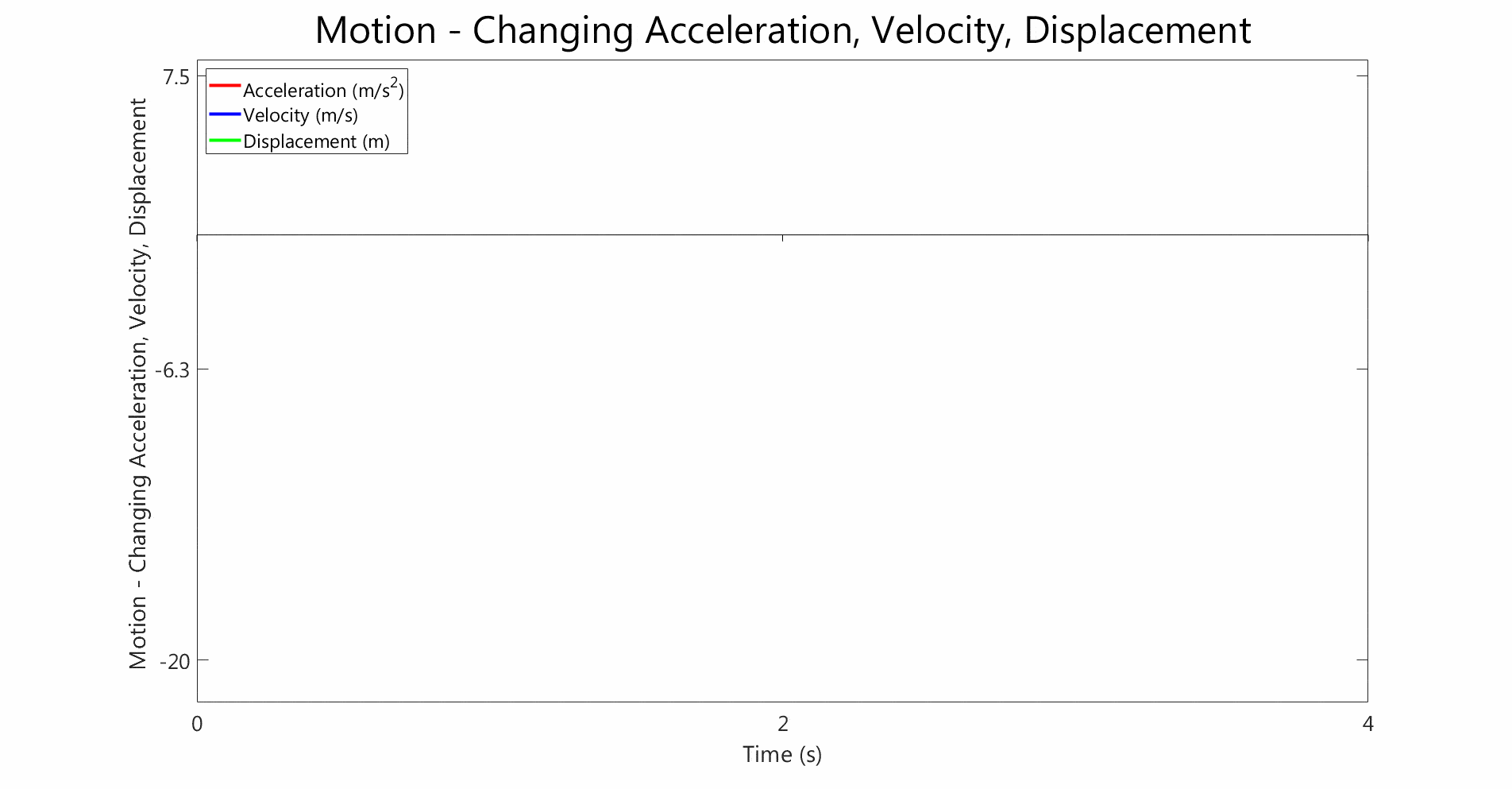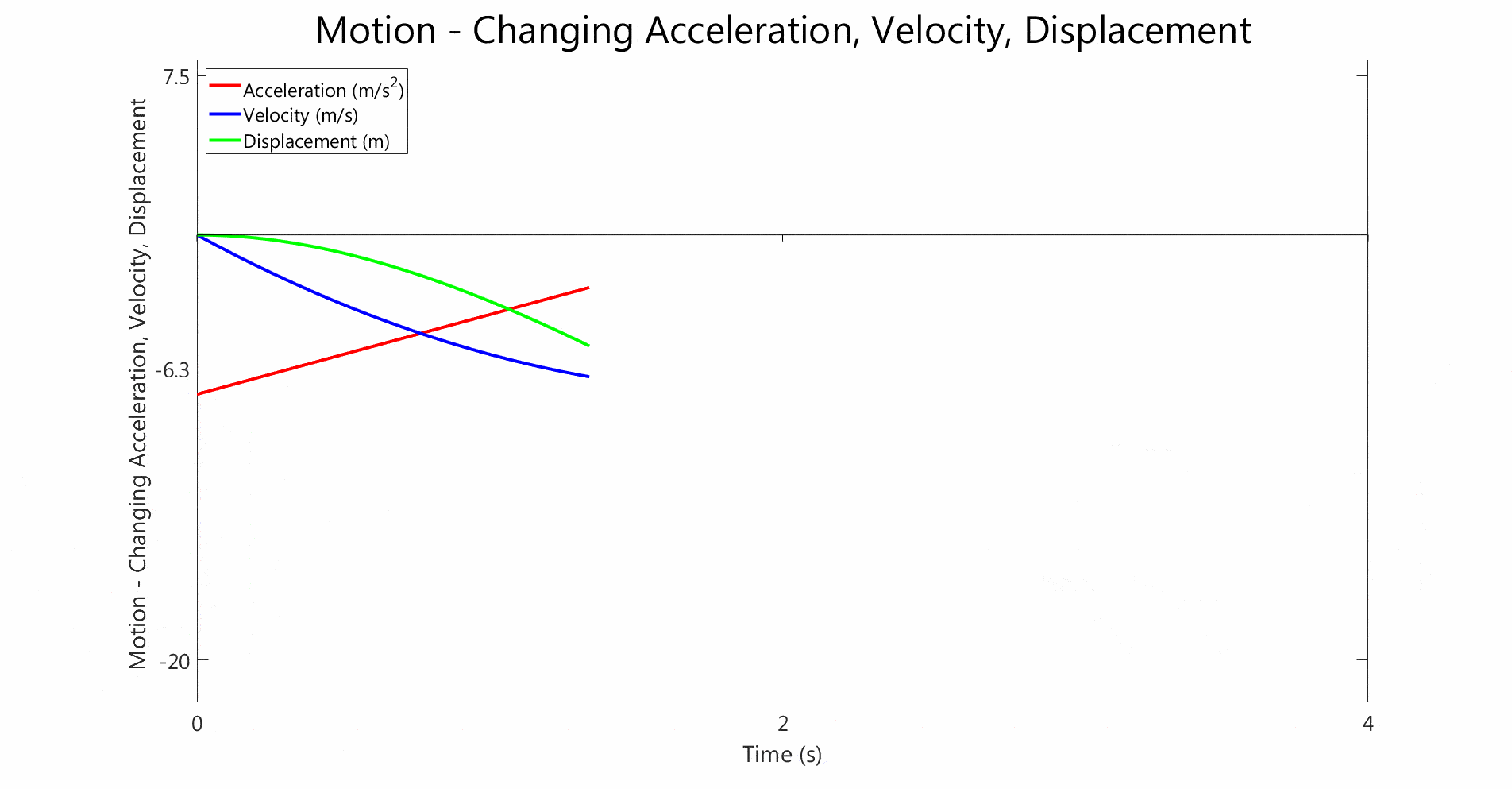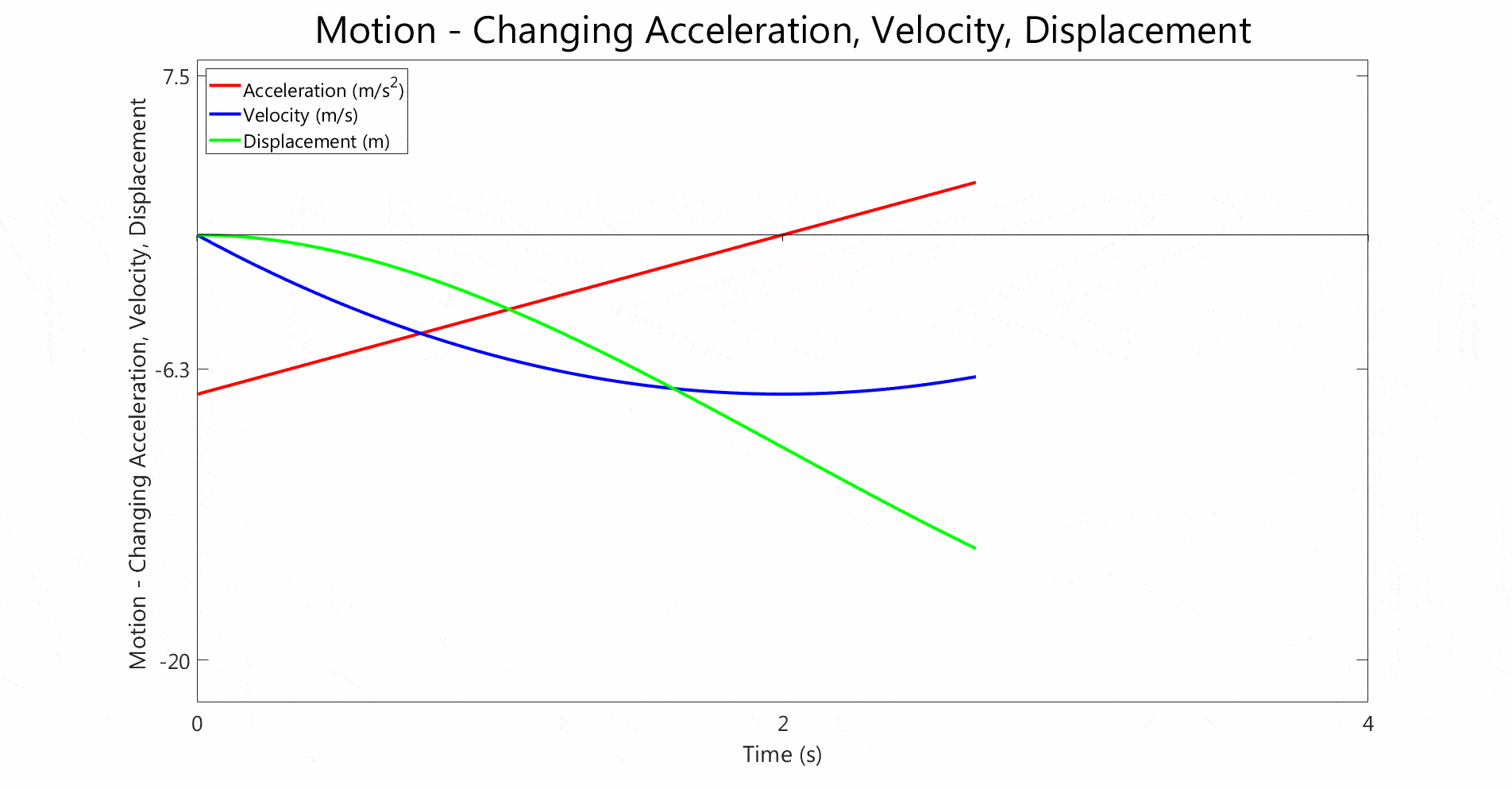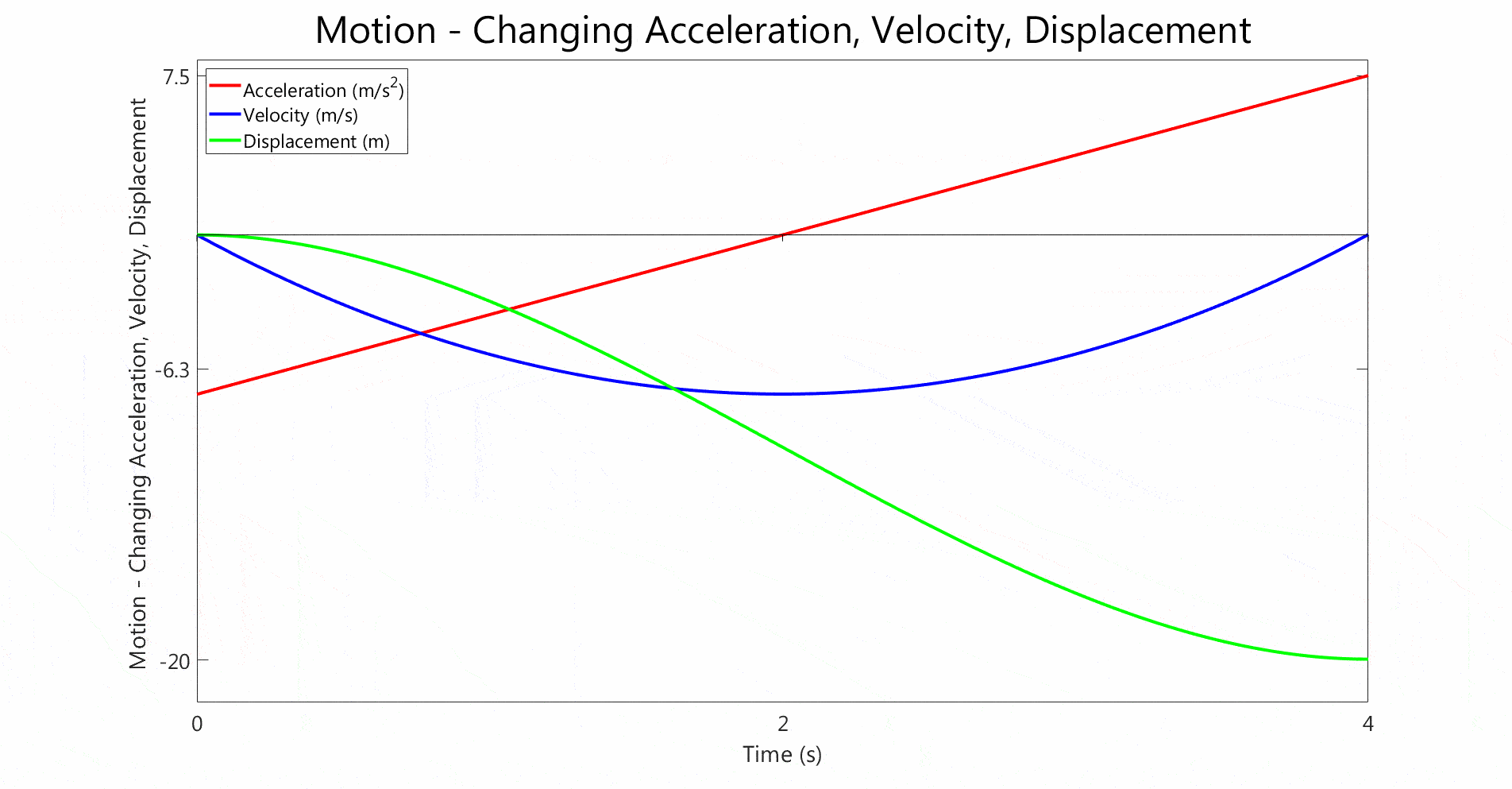
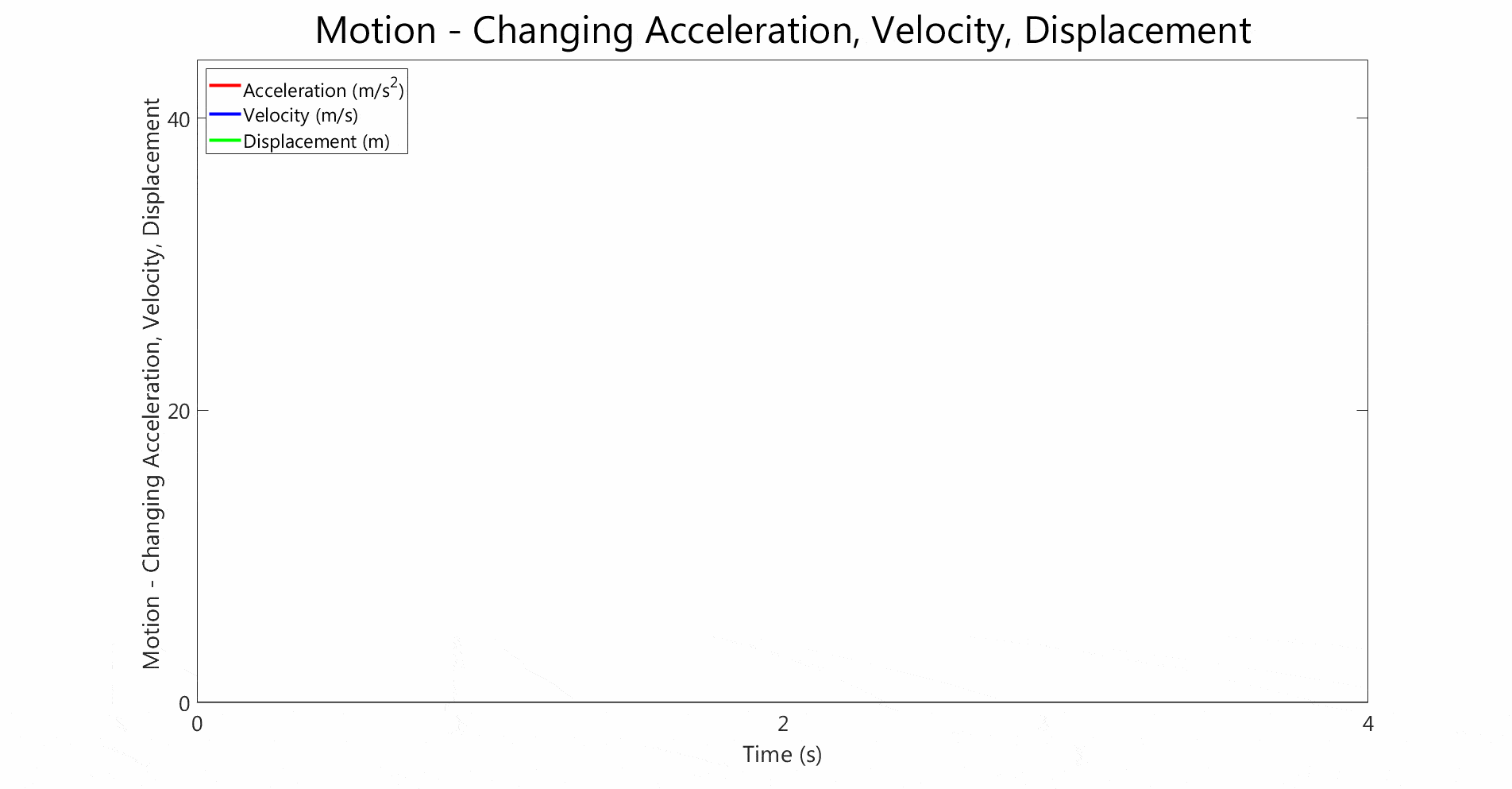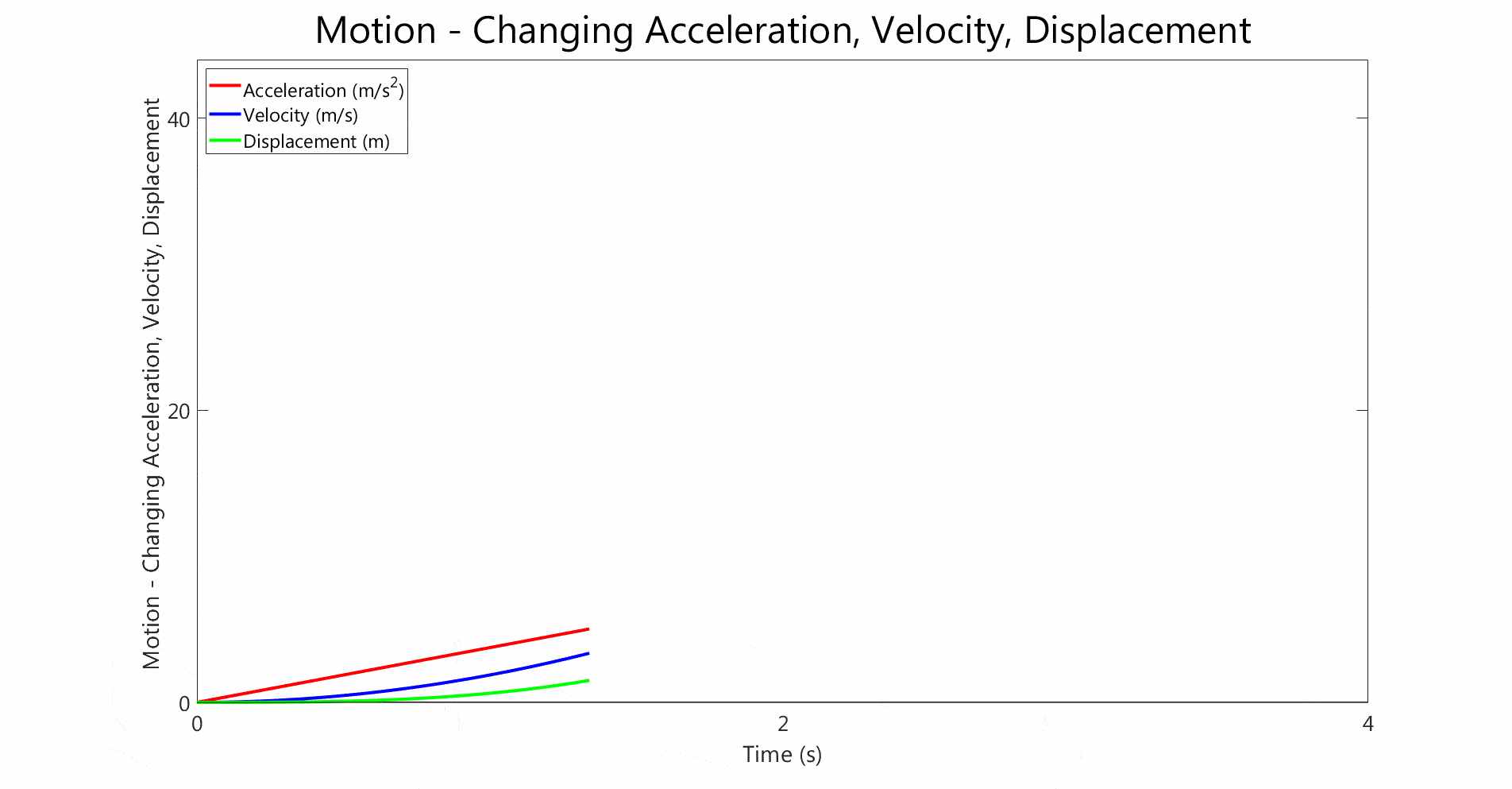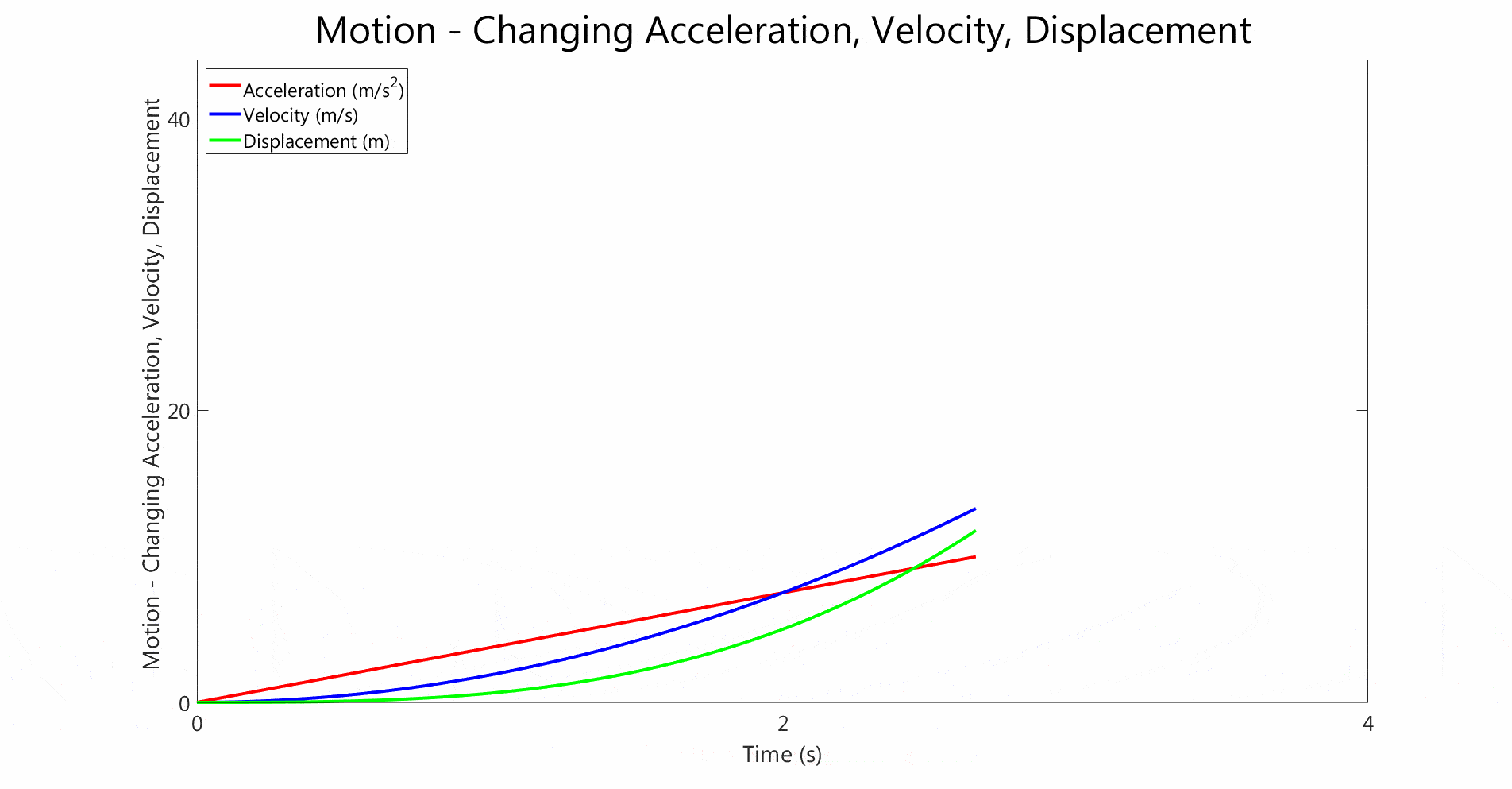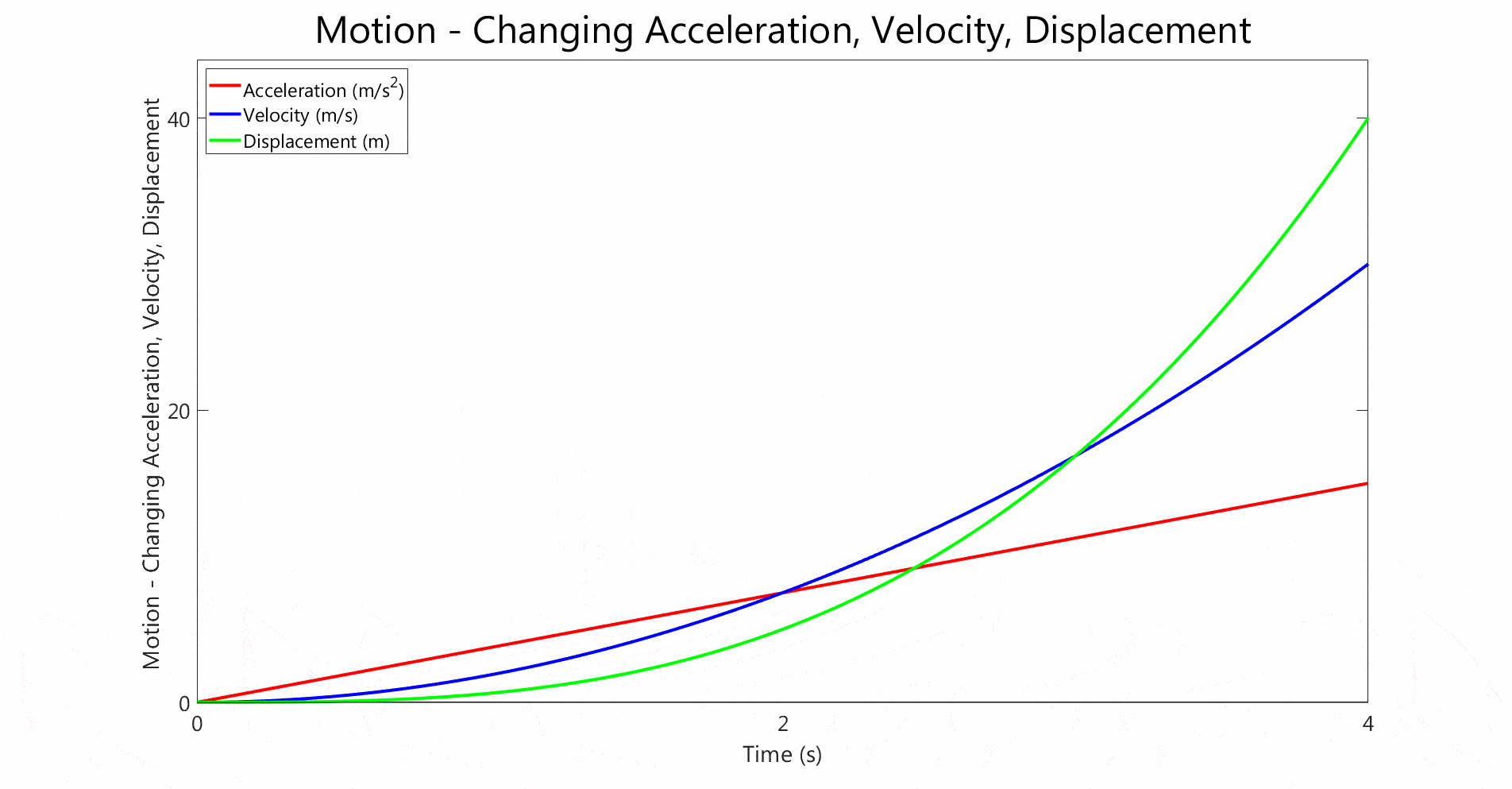
Both graphs show non-constant acceleration.
The acceleration changes linearly with time in both cases
In the first graph, the acceleration is initially negative, i.e. the body is under deceleration, and linearly increases. Halfway through it crosses 0 and changes to positive, and the body starts accelerating.
- The velocity follows a quadratic curve,
- The displacement curve is even steeper than the velocity curve
In the second graph, the acceleration starts from 0 and linearly increases.
- The velocity follows a quadratic curve,
- The displacement is even steeper than the velocity curve