Physics 101

Course sections

Section 1
Momentum
1
Momentum

Momentum

Momentum

Momentum and Impulse

Momentum

  • It is the product of mass and velocity of an object
  • It is a vector quantity
  • p = m \times v
  • SI unit is kg \cdot m/s or N \cdot s

Impulse

  • Impulse is the product of force and the time for which it acts.
  • It is a vector quantity
  • I = F \times t
  • SI unit is N \cdot s
  • From F = ma \rightarrow
    • a = \frac{v-u}{t}
    • F = m \times \frac{v-u}{t}
    • F = \frac{mv - mu}{t}
    • \mathbf{\mathit{Ft = mv - mu}}
  • Thus, impulse is the change in momentum.

Law of Conservation of Momentum

  • The total momentum of an isolated system remains constant.
    • Isolated System – Net External Force = 0 N
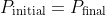
  • P_\textup{initial}=P_\textup{final}
  • m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2
    • m_1, m_2 are the masses of the two bodies in the system
    • u_1, u_2 are their initial velocities
    • v_1, v_2 are their final velocities

 

  • Example: Gun firing a bullet
    • Before the Gun fires the bullet, the net momentum of the system is 0.
    • After the gun fires,
      • the bullet travels to the right,
      • the recoil from the gunshot pushes the gun to the left.
    • The total momentum of the system remains 0,
      • The velocity of the gun, which has a much larger mass, is low
      • The velocity of the bullet, which has a much smaller mass, is high

Momentum and Impulse Application

Example: Ball hits the wall and rebounds

  • Initially, the striking cue imparts momentum to the cue-ball (M1)
  • The cue ball (M_{1}, u_\textup{1.1}) collides (1) with the stationary red ball (M_{2}, u_\textup{2.1})
  • The cue ball comes to a rest (M_{1}, v_\textup{1.1}), while the stationary red ball (M_{2}, v_\textup{2.1}) moves towards the wall
  • The red ball collides (2) with the wall (M_{2}, u_\textup{2.2}) and rebounds at a lower speed (M_{2}, v_\textup{2.2})

Practice Question: Given –

  • M_{1} = M_{2} = 0.2kg
  • u_{1,1} = 4 \frac{m}{s}
  • v_{2,2} = 3 \frac{m}{s}
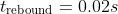
  • t_\textup{rebound}=0.02 s
  • Calculate the Force acting on the ball as it rebounds off the wall.

Solution:

Assuming Left is Positive

  • Governing equation of conservation of momentum:
    • M_1 u_1+M_2 u_1=M_1 v_1+M_2 v_2
  • First collision:
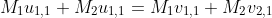
    • M_1 u_\textup{1,1}+M_2 u_\textup{1,1}=M_1 v_\textup{1,1}+M_2 v_\textup{2,1}
    • 0.2(4)+0.2 (0)=0.2(0)+0.2(v_\textup{2,1})
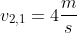
    • v_\textup{2,1}=4 \frac{m}{s}
    • Note: When objects of the same mass collide, and one of them was stationary, then the moving object comes to a complete rest while the stationary object gains all the velocity of the moving object.
  • Second collision:
    • Here, conservation of momentum does not apply:
      • M_2 u_\textup{2,2} \neq M_2 v_\textup{2,2}
      • 0.2(4) \neq 0.2(3)
    • This is because there is a net force acting on the system: Impulse from the rebound
  • Calculating Force from Impulse:
    • F_I= \frac{ M_2(v_\textup{2,2}-u_\textup{2,2})}{t_\textup{rebound}}
    • F_I= \frac{ 0.2(-3-4)}{0.02}
    • F_I= -70N
    • The Force is Negative: this means that the force is acting opposite to the originally assumed positive direction.
      • Assumption: Left is positive
      • Thus, the force is of magnitude \mathbf{70N} and acting to the Right
    • This makes sense, since in order to change the direction of the ball to the right, the Force has to act towards the right.